This post is part of a series of posts describing practical use of the M-209 cipher machine. The series will cover operation of the machine, setting the cipher key, formatting of messages, ciphering and deciphering messages, dealing with transmission errors, practices to make cryptanalysis (code breaking) of messages more difficult, and generating new key tables.

This chapter covers cryptographic basics to help you understand the machine.

The M-209 is a cipher machine designed by Boris Hagelin, and used by U.S. forces during World War 2 for encryption of lower level traffic. It was known to be breakable by German forces, but it was still useful for low-level, high-volume traffic that only needed to be protected for a matter of hours. More details about the machine’s functioning and history can be found online at many places including Wikipedia and my own web page. M-209 machines are available on the surplus market, but they are somewhat rare and expensive (despite being among the least expensive cipher machines available). If you do not have access to a real one, you can use a simulator such as this excellent graphical simulator for Windows computers or the command-line simulator I wrote to help me understand the machine better.

Chapter 1:  Cryptographic Basics  (this post)
Chapter 2:  Operating the M-209
Chapter 3:  M-209 Under the Covers
Chapter 4:  Enciphering Messages
Chapter 5:  Deciphering Messages
Chapter 6:  When Things Go Wrong  (coming soon)
Chapter 7:  Making Things Harder for the Enemy  (coming soon)
Chapter 8:  Creating Key Tables  (coming soon)

 

---

Chapter 1: Cryptographic Basics

Before we get into the machine itself, I’ll cover some basics of cryptography in case you don’t have prior experience with codes and ciphers. This post will barely scratch the surface of even the simplest amateur cryptography, but I hope it will give you the foundation to understand what the M-209 does, and why it does it. If you would like to learn a lot more about making and breaking codes and ciphers, you might wish to start with Kahn’s The Codebreakers and Schneier’s Applied Cryptography.

Codes and Ciphers

Codes and ciphers are used to hide messages from your adversaries, and hopefully make them only readable by your allies. Codes obscure messages by replacing entire words or phrases with different words, phrases or symbols. Historically, codes were often implemented by creating thick code books which listed large numbers of words and phrases, tabulated with code words, symbols or numbers that correspond to them. These days, codes have been mostly replaced by ciphers, which operate on the individual letters of a message rather than entire words and phrases. Steganography is the art and science of hiding the fact that a secret message even exists. This post will focus only on ciphers.

A cipher converts a readable plaintext message into an incomprehensible ciphertext (and vice versa) by combining it with a key and operating on it with a cryptographic algorithm. Practical and secure cipher methods assume that your adversary is aware of the cipher’s algorithm, but will be unable to decipher the ciphertext in a reasonable amount of time without knowing the corresponding key.

Many cipher algorithms are considered classified and are kept secret. However, cryptographic experts today generally consider it unwise to rely on secrecy of a cryptographic algorithm for security. Instead, they advise publishing proposed algorithms so that they can be examined for weaknesses by many experts in the field, and found to be suitably secure against attack without knowledge of the cipher key. The M-209 provides a good example of this, as machines implementing its cryptographic algorithm were commercially available prior to its use by the U.S. military. Thus, its algorithm was known (or at least knowable) by all adversaries, yet it still provided useful security.

Substitution Ciphers

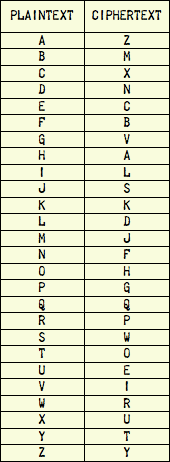
An easy cipher to understand is the substitution cipher. Its simplest form is called a simple substitution cipher. In this cipher, we simply map a plaintext alphabet to a ciphertext alphabet with a fixed table like this one:

If we enciphered the phrase “HELLO WORLD” with this particular cipher, the result would be “ACDDH RHPDN”. The specific mapping of plaintext letters to ciphertext letters is arbitrary, but the sender and recipient both need to use the same table to communicate successfully. Or at least they would if this simple cipher was any good, which it is not…

If we use the same table for each letter in the plaintext, then the cipher is called a monoalphabetic substitution cipher. If we use a different table for each letter in the plaintext, then it’s a polyalphabetic substitution cipher. Monoalphabetic substitution cipher’s are extremely weak. They’ve often been offered as puzzles in newspapers, and they can be broken with elementary techniques of cryptanalysis described in children’s books. Their biggest weakness is that they do not obscure the relative letter frequencies of the language they’re enciphering (for example, in English the letter “E” is used more commonly than any other letter), so a single ciphertext can be broken by merely knowing (or guessing) the language of the plaintext and that language’s relative letter frequencies. The “HELLO WORLD” example above would be hard to break because it is so short, but a message of any useful length can usually be broken easily if it is enciphered with a simple monoalphabetic substitution cipher.

The M-209

The M-209’s algorithm implements a polyalphabetic substitution cipher. Each character of plaintext is mapped to one of 26 different ciphertext alphabets (technically 28 alphabets, but two pairs of them match each other), and those ciphertext alphabets are used in a complex sequence which extends for 101,405,850 characters before repeating. The specific sequence is determined by a key which describes how to set a number of pins and lugs inside the machine, and each message starts at a different point in the sequence which is determined by setting the six wheels on the front of the machine.

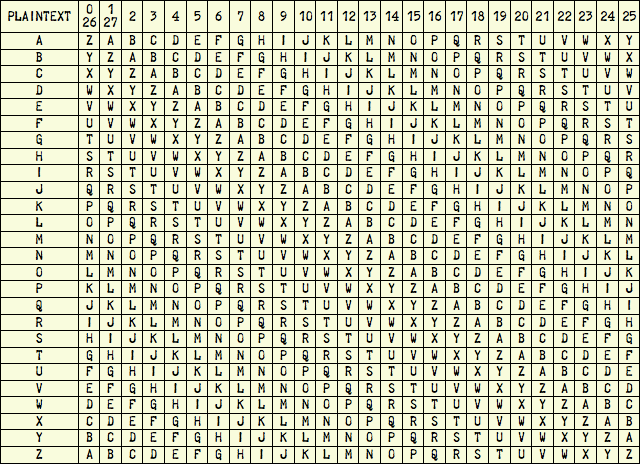
Each ciphertext alphabet is simply the reciprocal of the plaintext alphabet (that is, ABC…XYZ replaced by ZYX…CBA) rotated by 0-27 places:

Why is this the case? Well, let’s peek inside the machine and take a quick look at how it works. Here’s a picture of the M-209 with its cover opened to show the internal parts:

When we operate the machine, we dial in each letter of the plaintext with the setting wheel (A) at the front left corner, and then turn the large drive knob (D) on the right side of the machine. The setting knob has the letters A through Z marked around its circumference and visible to the operator (B), and metal type (C) letters Z through A around its circumference under the inner cover. Turning the setting wheel to marked letter A, for example, lines up the type letter Z with the printing mechanism, setting to marked letter B lines up type letter Y, etc. By itself, this would implement a weak monoalphabetic substitution cipher, using the alphabet in the 0/26 column in the table above. However, when the operator turns the drive knob, the machine picks a number between 0 and 27 based on the settings of the pin wheels (E) and lug drum (F), and then turns the setting knob by that number of clicks before printing the ciphertext letter onto paper tape. Turning the wheel like that before printing effectively selects one of the 26 different cipher alphabets in the above table. After printing the enciphered letter, the machine advances the pin wheels (E), so that a different ciphertext alphabet will be selected for the next letter of the message.

I won’t get into the details in this series, but the M-209 uses reciprocal alphabets instead of ones in normal or scrambled order because that happens to make this particular cipher a symmetric-key algorithm, meaning that the sender and recipient both use the same key to encipher and decipher the message. There are other kinds of ciphers in which you need to use different (but complementary) keys for enciphering and deciphering messages, and these ciphers are commonly used for public-key cryptography.

So, an attacker knows that only one of 26 possible ciphertext alphabets are used for each character of the message, but he doesn’t know the order in which they’re used. The key wheels (E) and lug drum (F) inside the machine generate a sequence of 101,505,850 numbers between 0-27, and then use those numbers to select one of 26 different ciphertext alphabets (remember, alphabets 0 and 26 are the same, as are alphabets 1 and 27). He knows the machine’s cryptographic algorithm, but he needs to figure out the complex settings of the pins (on wheels E), lugs (on drum F) and starting wheel (E) positions to determine the sequence in which the ciphertext alphabets are applied to the plaintext. This is pretty hard to do, but as we’ll see later, it’s not impossible… especially when there’s a lot of message traffic to analyze and code clerks make mistakes to give the adversary openings into the cipher.

Readers who are familiar with pseudorandom number generators (PRNGs) may realize that the wheels and drum of the M-209 implement a PRNG. The specific number sequence is determined by the pin and lug settings. The initial positions of the wheels at the start of a message determine the PRNG’s seed.

In summary, the M-209 implements a particular cryptographic algorithm for converting plaintext into ciphertext, and vice versa. The key consists of the internal pin and lug settings, and the initial settings of the six wheels at the start of a message. In practice, the pin and lug settings would be changed daily and used by many cipher clerks in an area of operations. Unique wheel settings would be selected for each individual message for various reasons we’ll cover later. There are many ways for a sender to select the initial wheel settings for an individual message and convey those settings to the recipient(s). One technique which is known to have been used by U.S. forces during World War 2 is for the sender to randomly select the starting wheel settings, and then encipher them and include the enciphered version at the beginning of the message using a technique that I will describe later.

So, now you know what the M-209 does, and a little bit about how it works. In the next chapter, I’ll describe how to operate the machine.